✅ 1. 트리

- 데이터 간의 관계를 나타내는 비선형 자료구조이다. ( 1:N 관계이며, 일직선이 아님 )
- 노드(node)라고 불리는 부분과 노드를 연결하는 가지(branch, edge)로 구분이 된다.
- 노드 사이에는 계층적인 관계성을 갖고 있고 이것은 레벨0, 1, 2, 3 등이 될 수 있음.
(1) 트리 용어 정의
- 노드(node): 정보 항목을 의미하며 A, B, C, D ... 등이 모두 노드가 될 수 있음.
- 루트(root): 빈 트리가 아닌 경우에 맨 꼭대기에 있는 하나의 노드를 의미함. ( A 부분에 해당함 )
- 차수(degree): 각 노드에 있는 가지의 수를 의미함. ( 그 노드가 가지고 있는 자식 노드(하위 노드)의 개수로 봐야 함. )
(2) 잎 노드 (단말 노드) & 내부 노드 (비단말 노드)

[ 잎 노드 ( 단말 노드 ) ]
- 단말 노드라고 불리며, 노드의 차수가 0인 노드 즉, 자식이 없는 노드를 의미한다. ( 3레벨에 해당 할 듯 )
[ 내부 노드 ( 비단말 노드 ) ]
- 비단말 노드라고 불리며, 루트 노드와 단말 노드를 제외한 나머지 노드를 의미한다. ( 레벨 1과 2가 해당 할 듯 )
(3) 조상 노드 & 자손 노드
[ 조상 노드 ]
- 루트 노드로부터 어떤 노드 X까지의 경로(가지들의 모음) 상에 존재하는 모든 노드를 X의 조상 노드라고 함.
- 쉽게말해, 특정 노드와 루트 노드 까지 이어지는 모든 노드를 조상 노드라고 부름.
[ 자손 노드 ]
- 어떤 노드 X에서 단말 노드까지의 경로 상에 존재하는 모든 노드를 자손 노드라고 함.
- 쉽게말해, 특정 노드의 아래에 연결 된 모든 노드를 자손 노드로 볼 수 있음. 즉, 루트의 자손이라 하면 전부다임.
(4) 레벨 & 깊이 개념

- 루트 노드로부터의 거리(가지의 수)를 의미한다. 0레벨 ~ N레벨 까지 존재 할 수 있음.
- 트리의 깊이 또는 높이로도 표현을 할 수 있으며, 루트 노드로부터 가장 긴 경로에 있는 단말 노드의 레벨에 1의 값을 더한 것이 될 수 있음. 즉, 레벨이 3레벨인 경우 깊이 4가 될 수 있음.
(5) 서브 트리 & 숲
[ 서브 트리 (subtree) ]

- 특정 노드를 루트 노드로 하고, 그 아래에 있는 연결된 구조의 트리를 의미한다.
- 이미지를 예시로 들면, 파란색 부분의 서브 트리는 빨간색 부분이 될 수 있음.
- 쉽게말해, 특정 노드의 서브 트리는 자식들의 갯수가 아닌 자식의 트리 구조를 서브 트리로 보는 것임.
[ 숲 (forest) ]
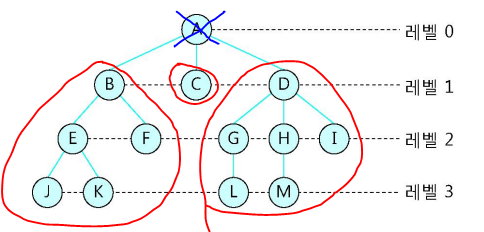
- n개의 서브 트리를 가진 트리에서 루트 노드를 제거해서 얻을 수 있는 분리된 서브 트리의 집합을 의미함.
- 핵심은 루트 노드를 제거한다고 가정을 해야하고, 제거가 된 상태에서 분리된 서브 트리의 집합들을 의미함.
- 쉽게말해, 분리된 서브 트리의 집합 형태의 구조로 보면됨. ( 서브 트리들을 묶어놓은 논리적인 개념? 이런 느낌임 )
✅ 2. 이진 트리 (Binary Tree)
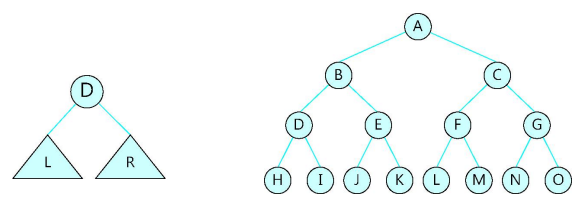
- 트리 중에서 차수가 2인 트리를 의미하며, 이진 트리의 조건은 모든 노드의 차수는 최대 2를 넘지 않아야 한다는 것이다.
- 즉, 모든 노드는 최대 2개의 서브 트리를 가질 수 있다는 의미로도 볼 수 있음.
- 각 서브 트리는 왼쪽 서브 트리와 오른쪽 서브 트리로 구분이 됨.
- 이진 트리에서 왼쪽 노드와 오른쪽 노드는 순서의 의미를 가지고 있으며, 이것을 이용해 탐색 할 때 사용이 되기도 함.
- 쉽게말해, 이미지의 노드의 알파벳의 순서를 보고 의미를 부여해 A -> B -> C 이런 관계로 볼 수도 있다는 의미임.
- 이진 트리의 각 서브 트리는 다시 이진 트리가 됨
(1) 이진 트리의 높이
[ 최대 높이 ]
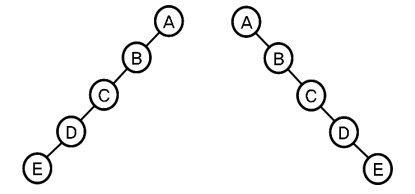
- N개의 노드를 가진 이진 트리의 높이를 계산으로 구할 수 있음
- 최대 높이: N으로 노드의 개수와 같음
- 쉽게말해, 같은 갯수의 노드를 갖는 이진트리가 최대 갯수가 되도록 만들려면 위 그림처럼 경사지게 만들어야 함.
- 즉, 경사지게 만들면 최대 높이가 항상 노드의 갯수와 같게 된다는 의미임. 즉, 이 구조가 최대 높이가 된다는 의미임.
[ 최소 높이 ]

- 모든 내부 노드가 최대 2개의 자식 노드를 갖는 경우로서 [log2N] + 1 이 높이가 됨.
- 2개의 노드를 갖는 구조를 최대한 꽉 채웠을 때 최소 높이가 될 수 있음.
(2) 이진 트리 순회 연산

- 결국 이진트리 또한 데이터를 저장하기 위한 자료구조임.
- 즉, 자료구조 이기 때문에 트리에서 자료를 저장하고 난 후 어떻게 검색 할 것 인지에 대한 연산이 필요함.
- 즉, 일정한 순서에 따라 트리에 있는 각 노드를 한 번씩 방문하도록 도와주는 순회 연산을 함.
[ DLR ( 전위 순회: preorder) ]
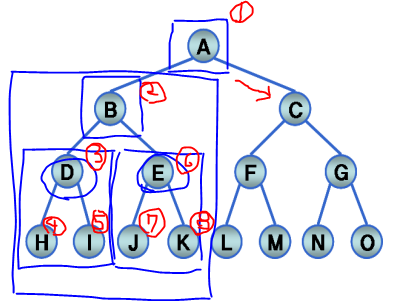
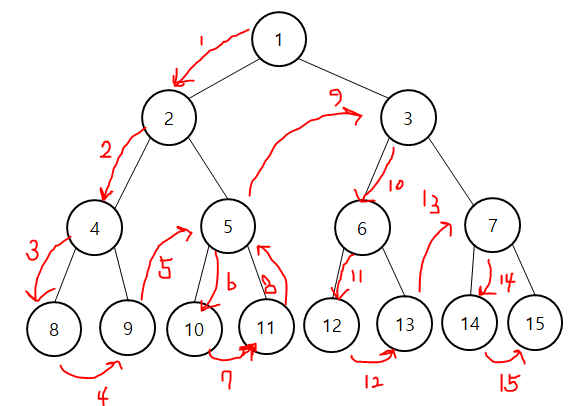
- DLR ( Data - Left - Right ) 을 의미하며, 왼쪽 이후 오른쪽을 처리한다는 의미를 가짐.
- 루트 노드 방문 -> 왼쪽 서브 트리 방문 -> 오른쪽 서브 트리 방문 하는 과정을 거치는 방식이다.
- 루트를 먼저가서 A 출력 -> 다음 트리의 루트인 B로 가서 B를 출력함 -> 그 다음은 D
- 전위 순회로 처리가 될 경우 이미지와 같이 A -> B -> D -> H -> I -> E -> J -> K -> C 순서로 처리가 되게 된다.
- 왼쪽 서브트리 모두 끝내고 오른쪽 서브트리 방문 형식
[ LDR ( 중위 순회: inorder) ]


- 왼쪽 서브 트리 방문 -> 루트 노드 방문 -> 오른쪽 서브 트리 방문 하는 과정을 거치는 방식임.
- 전위는 루트 노드가 제일 먼저 시작이 되었다면 중위 방식은 루트 노드가 가운데에 들어가는 방식임.
- 가운데 서브 트리의 루트 노드가 가운데로 들어가게 됨.
[ LRD ( 후위 순회: postorder) ]

- 왼쪽 서브 트리 방문 -> 오른쪽 서브 트리 방문 -> 루트 노드 방문 하는 과정을 거치는 방식임.
(3) 포화 이진 트리 (Full Binary Tree)

- 깊이가 k인 이진 트리 중에서 노드의 개수가 2^k - 1 개인 이진 트리를 의미한다.
- 깊이가 k인 이진 트리가 가질 수 있는 최대 개수는 2^k - 1개 이며, 단말 노드의 개수가 2^k - 1 개
- 즉, 모든 내부 노드가 자식을 2개씩 가지고 있는 경우이며, N레벨에 맞게 노드가 꽉차있는 경우임.
- 정리하면, 각 레벨에서 빈자리가 없이 노드를 모두 가지고 있는 경우에 모든 내부 노드들은 2개의 자식 노드를 가지는 경우임.
(4) 완전 이진 트리 (Complete Binary Tree)


- 트리의 최대 레벨이 k 일 때, 레벨 k-1까지는 포화 이진 트리를 형성하고, 레벨 k에서는 왼쪽부터 오른쪽으로 채워진 트리임
- 총 노드의 개수가 2^k+1 - 1 을 초과하지 않으면서, 포화 이진 트리의 노드 번호에 해당하는 연속적인 번호를 갖는 트리임.
- 쉽게말해, 마지막 레벨을 제외한 모든 레벨이 꽉 차 있는 경우이며, 마지막 레벨은 왼쪽부터 채워진 이진 트리를 의미함.
- 왼쪽부터 연속적으로 채워지는 상태여야 함. 즉, F 밑에 먼저 K가 들어오는 경우라면 E 밑에는 비어있으므로 아님.
- 또한, 모든 포화 이진 트리는 와전 트리로 볼 수 있으며, 모든 완전 이진 트리는 포화 이진 트리는 아닐 수 있는 관계를 가짐.
- 쉽게말해, 모든 노드가 다 차있으면 포화 이진 트리 이면서, 완전 이진 트리로 볼 수 있음.
(5) 경사 이진 트리 (Skewed Binary Tree)
- 한 쪽 방향으로만 가지가 뻗어 나간 이진 트리를 의미함.
- 왼쪽 방향으로만 가지가 뻗어 나간 경사 이진 트리 또는 오른쪽으로만 가지가 뻗어 나간 경사 이진 트리가 있음.
- 같은 갯수의 노드를 갖는 상태에서 깊이가 가장 큰 이진 트리를 만들 수 있는 방법은 경사 이진 트리를 만드는 것이다.
(6) 정리하면
- 트리 자료구조: 계층 구조를 표현하기 위해 노드들을 연결한 자료구조이며, 기본적으로 노드, 류트, 자식 노드, 부모 노드, 잎 노드, 간선, 차수, 레벨이 존재함. 또한, 모든 노드는 루트 노드로부터 연결되어 있으며, 사이클이 없는 구조이며, 트리의 대표적인 종류로는 이진 트리, 완전 이진 트리, 포화 이진 트리, 이진 탐색 트리 등이 있음.
- 이진 트리, 완전 이진 트리, 포화 이진 트리, 이진 탐색 트리 등은 결국 트리 라는 자료구조의 기본적인 구조를 가지고 파생 된 자료구조로 볼 수 있음.
- 포화 이진 트리와 완전 이진 트리는 이진 트리에서 구조적 제약을 둔 파생으로 볼 수 있음.
- 이진 탐색 트리는 값의 규칙을 둔 파생으로 볼 수 있음.
- 이진 트리의 순회 연산: 이진 트리에 저장된 데이터를 읽는 방법인 즉, 알고리즘이며 이진 트리 전용 알고리즘으로 볼 수 있음.
✅ 3. 그래프

- 정점(vertex) 들의 유한 집합 V와 두 개의 정점을 연결하는 간선(edge)들의 유한 집합 E로 정의
- G=(V,E)로 표시가 됨. ( vertex = node 라고도 불림 )
(1) 무방향 그래프 (undirected graph)

- 간선이 방향성이 없는 간선으로 연결된 그래프를 의미하며, 방향이 없기 때문에 양방향으로 이동이 가능함.
(2) 방향 그래프 (directed graph)

- 두 정점을 연결하는 간선이 방향성을 가지는 간선으로 연결된 그래프를 의미한다.
- 즉, 방향이 있는 곳으로만 갈 수 있으며, 없는 경우에는 이동은 불가능하다는 의미임.
(3) 그래프의 집합 표현 방법

- V 는 정점, E 는 간선을 의미함
- 무방향 그래프인 경우 "()" 소 괄호로 표현이 되며, 방향 그래프는 "<>" 꺽새로 표현이 된다.
- 또한, 무방향 그래프에서는 양방향을 가르키기 때문에 1,4 또는 4,1 둘 중 하나만 사용을 해 중복을 없앤다.
(4) 그래프의 용어
- 두 정점이 간선으로 직접 연결되어 있으면 두 정점은 인접(adjacent)해 있다고 하며, 해당 간선은 두 정점에 부수(incident) 되었다고 함.
- 인접한다: 정점 간의 관계를 의미함.
- 부수되었다: 정점과 간선 간의 관계를 의미함.
- 쉽게말해, "인접한다" 는 두 정점이 간선으로 직접 연결되어 있음을 의미하고, "부수되다" 는 이 간선이 이 정점에 연결되어 있다 라는 의미를 가지고 있는 것임.
[ 경로(path) ]
- 간선으로 연결된 정점들의 순차적 나열을 의미한다.
- 예시: A -> B -> C -> D ( A 에서 시작해 B, C를 거쳐 D로 가는 길을 의미함 )
[ 경로의 길이 ]
- 경로에 포함된 간선의 개수로 표현을 함.
- 예시: A -> B -> C -> D ( 간선은 A-B, B-C, C-D 이렇게 총 3개, 따라서 길이 = 3 이 됨. )
[ 단순 경로(simple path) ]
- 중복된 정점 없이 연결된 경로를 의미하며, 경로 상에 존재하는 정점들이 모두 다른 경로로 볼 수 있음.
- 쉽게말해, 같은 집을 두 번 들르지 않고 길을 가는 것
- 예시: A -> B -> C -> D -> E ( 중간에 같은 정점이 없으면 단순 경로가 됨 )
[ 사이클(cycle) ]
- 세 개 이상의 정점을 가진 경로 중에서 시작 정점과 끝 정점이 같은 경로를 의미함. ( 즉, 원을 이루는 경로임 )
- 단순 사이클이 아니므로 중복이 되는 정점이 있을 수 있음.
- 예시: A -> B -> C -> A ( A에서 시작해서 B, C를 거쳐 다시 A로 돌아오는 길 )
[ 단순 사이클(simple cycle) ]
- 중복된 정점 없이 시작점으로 돌아오는 사이클을 의미하며, 시작 정점과 끝 정점을 제외하고 모든 정점이 다른 사이클
- 쉽게말해, 원을 돌되, 한 번 들른 정점은 다시 지나지 않겠다는 의미임.
- 예시: A -> B -> C -> A = 단순 사이클 / A -> B -> C -> B -> A = 그냥 사이클로 보면 될듯.
[ 두 정점은 서로 연결되었다 ]
- 두 정점 사이에 경로가 존재한다는 의미임. ( 즉, 갈수만 있으면 연결되었다고 표현하는 듯 )
[ 그래프가 서로 연결되었다 ]
- 무방향 그래프에서 서로 다른 모든 정점들 사이에 경로가 존재함 ( 모든 정점들이 연결 된 상태 )
[ 무방향 그래프에서 한 정점의 차수 ]
- 정점에 부수된 간선의 개수를 의미함. ( 즉, 정점에 붙어있는 간선의 개수를 의미함 )
[ 방향 그래프 정점의 차수는 진입 차수와 진출 차수로 나뉨 ]
- 진입 차수(indegree): 다른 정점에서 해당 정점으로 향하는 간선의 개수를 의미함.
- 진출 차수(outdegree): 해당 정점에서 다른 정점으로 향하는 간선의 개수를 의미함.
- 쉽게말해 방향이 있는 그래프에서 특정 정점으로 나가는 차수는 진출 차수, 들어오는 차수를 진입 차수로 볼 수 있음.
[ 트리와 그래프 ]
- 트리는 그래프의 특수한 형태로 봄 즉, 사이클이 존재하지 않아 계층적인 구조가 가능함
- 무방향 그래프에서 모든 정점이 서로 연결되어 있으면서 사이클이 존재하지 않는 그래프를 트리라고 함.
✅ 4. 그래프의 표현
- 그래프를 컴퓨터 프로그래밍 언어로 구현하기 위해서는 인접 행렬(adjacency matrix) 이나 인접 리스트(adjacency list)를 이용하여 표현함.
- 인접 행렬을 이용하여 n개의 정점을 가진 그래프를 표현하기 위해서는 n * n 크기의 2차원 배열을 이용함.
- 인접행렬 A[i][j] 에 값이 존재하면 그래프의 정점 vi 에서 정점 vj사이에 간선이 존재함을 의미하고, A[i][j]의 값은 1로 정함
(1) 인접행렬
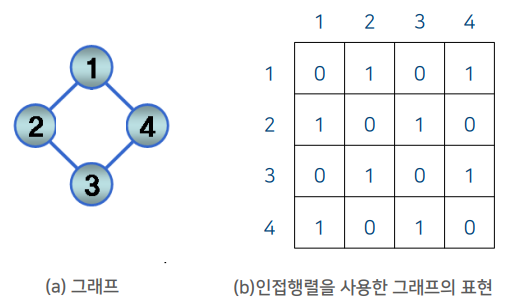
- (1,2) , (1,4) 가 연결이 된 상태이며, 오른쪽 인접행렬을 사용해 표현을 하면 1,2 와 1,4 에 숫자 1이 들어가게 된다.
- 연결이 되어 있지 않는 부분에는 0이 들어가게 된다.
(2) 인접리스트
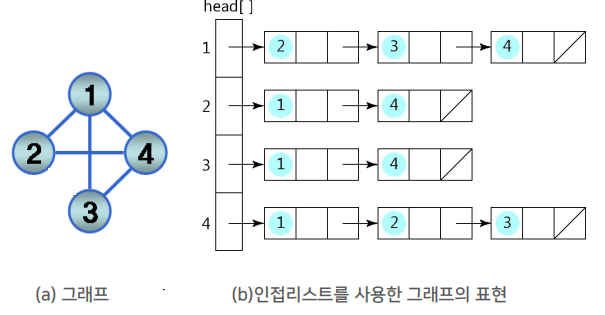
- 리스트를 활용하여 각각의 정점들이 인접해있는 정점들을 리스트로 표현한 것이다.
(3) 그래프의 탐색
- 그래프의 모든 정점을 체계적으로 방문하는 것을 의미한다. 쉽게말해, 트리의 순회와 비슷하다고 보면 됨.
- 그래프의 탐색은 깊이 우선 탐색(depth first search) 과 너비 우선 탐색(breadth first search) 이 있음.
(4) 깊이 우선 탐색

- 최근의 방문하지 않은 인접한 하나의 정점을 우선적으로 방문하는 방식이다.
- 최종적인 방문 순서는 (1, 2, 4, 5, 7, 6, 3) 이 됨.
- 최종 방문 순서는 구현 방법에 따라 달라질 수 있음
- 깊이 들어가는 것을 우선 순위로 두기 때문에 1 -> 2 -> 4로 내려간 뒤 5 -> 7 식으로 제일 깊은곳 까지 갔다가 돌아옴
- 1에서 아무 간선 2, 3 둘 중 하나 잡고 내려가는 느낌임.
(5) 너비 우선 탐색

- 최근의 방문하지 않은 인접한 모든 정점을 모두 방문하는 방식임.
- 최종적인 방문 순서는 (1, 2, 3, 4, 5, 6, 7) 이 될 수 있음.
- 최종 방문 순서는 구현 방법에 따라 달라질 수 있음
- 처음 1에서 2, 3을 다 출력하고 2를 선택해서 4, 5 출력하고 3에가서 6을 출력 한 뒤 마지막 7을 출력함
'🎓방송통신대학교 > 💻컴퓨터과학 개론' 카테고리의 다른 글
| [컴퓨터과학 개론] 6강 - 알고리즘(2) (0) | 2025.11.10 |
|---|---|
| [컴퓨터과학 개론] 5강 - 알고리즘(1) (0) | 2025.11.10 |
| [컴퓨터과학 개론] 3강 - 자료구조(1) (0) | 2025.09.17 |
| [컴퓨터과학 개론] 2강 - 컴퓨터와 자료(2) (0) | 2025.08.22 |
| [컴퓨터과학 개론] 1강 - 컴퓨터와 자료(1) (3) | 2025.08.20 |